代码随想录——数组篇

5 minute read

Published: November 06, 2024

本文记录了本人在Leetcode上练习代码随想录——数组篇的代码、心得、思路和体会，以便后续复习和查看。如果遇到有缘人，也可一起讨论和思考。本文也可在知乎上查看。

秉承着学习就是不断重复的过程，本文记录了本人在Leetcode上练习代码随想录——数组篇的代码、心得、思路和体会，以便后续复习和查看，如果遇到有缘人，也可一起讨论和思考。

二分查找

704. 二分查找 - 力扣（LeetCode）

此题是二分查找的典型例题，使用模板即可完美解决。由于本人在以往已经记住了两个二分查找模板（貌似来自洛谷，具体忘记了），故未使用代码随想录所用的模板。下面的模板适用于找到第一个大于等于目标值元素的下标，即从左往右寻找，如果找不到目标值，left的值是第一个大于目标值元素的下标，反之即为目标值元素的下标。使用这个模板即可完美解决这个题目了。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size()-1;
        while(left<right){
            int mid = (left+right)>>1;//即(left+right)/2
            if(nums[mid]<target)left = mid+1;
            else right=mid;
        }
        if(nums[left]==target)return left;
        else return -1;
    }
};

与上述模板对应的另一个模板适用于找到第一个小于等于目标值元素的下标，即从右往左寻找，如果找不到目标值，left的值是第一个小于目标值元素的下标，反之即为目标值元素的下标。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size()-1;
        while(left<right){
            int mid = (left+right+1)>>1;//即(left+right+1)/2
            if(nums[mid]>target)right = mid-1;
            else left=mid;
        }
        if(nums[left]==target)return left;
        else return -1;
    }
};

这两个模板其实是非常好记的，不同的点就两部分，一是mid的求法，二是如何更新left和right。记忆方法是从左往右找，left要加1，从右往左找，right要减1，mid计算也要加1。

35. 搜索插入位置 - 力扣（LeetCode）

此题是经典二分查找的简单变式，无论是使用第一个模板还是第二个模板都是可以写出来的，唯一需要注意的点就是要进行特判，若使用第一个模板，我们要判断原有数组的最大值是否小于目标值，如果是，要单独处理，即直接返回原有数组的长度。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        //如果比最大值还大，不特殊处理的话，下面的代码会返回n-1，而不是n
        if(nums[n-1]<target)return n;
        int left = 0;
        int right = n-1;
        while(left<right){
            int mid = (left+right)>>1;
            if(nums[mid]<target)left=mid+1;
            else right=mid;
        } 
        if(nums[left]==target)return left;
        else return left;
    }
};

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

此题也是二分查找的变式，使用上述提到的两个模板，即可完美解决，唯一需要注意的是如果使用本人的这两种模板需要进行特判，判断数组是否为空，如果为空，直接返回即可，貌似使用其他模板没有特判环节。

/*
如何返回题目要求的格式？有三种方法：
1.return ans //ans是vector类型
2.return vector<int>{1,2}
3.return {1,2}
*/
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        //需要进行特判，如果不进行特判，下面的代码nums[left]会报错
        if(!nums.size())return vector<int>{-1,-1};
        int left = 0;
        int right = nums.size()-1;
        while(left<right){
            int mid = (left+right)>>1;
            if(nums[mid]<target)left=mid+1;
            else right=mid;
        }
        if(nums[left]==target){
            int begin = left;
            left = 0;
            right = nums.size()-1;
            while(left<right){
                int mid = (left+right+1)>>1;
                if(nums[mid]>target)right=mid-1;
                else left=mid;
            }
            return vector<int>{begin,right};
        }
        else return vector<int>{-1,-1};
    }
};

69. x 的平方根 - 力扣（LeetCode）

此题也是二分查找的变式题，使用第一个模板即可完美解决，如果数x的算术平方根是整数，则可直接返回，若不是整数，则返回找到的下标值减1。此题最大的坑点在于计算过程中，由于数据x的范围比较大，这导致如果全程使用int类型，会出现数据溢出的现象，因此需要在计算的过程中，将int型转化为long long型。

/*
在转换数据类型时，犯了一个错误：
//mid是int，下面这个式子的计算过程是计算完mid*mid后，再将结果转换为long long，因此并不能防止数据溢出。
long long int temp = mid*mid
*/
class Solution {
public:
    int mySqrt(int x) {
        int left = 0;
        int right = x;
        while(left<right){
            int mid = (left+right)>>1;
            if((long long)mid*mid<x)left=mid+1;//将mid的int转化为long long再计算，计算就会按long long计算
            else right=mid;
        }
        if((long long)left*left==x)return left;
        else return left-1;
    }
};

367. 有效的完全平方数 - 力扣（LeetCode）

这道题简直和69. x 的平方根 - 力扣（LeetCode）一模一样，就是题目要求的返回值不同。

class Solution {
public:
    bool isPerfectSquare(int num) {
        int left = 0;
        int right = num;
        while(left<right){
            int mid = (left+right)>>1;
            if((long long)mid*mid<num)left = mid+1;
            else right = mid;
        }
        if((long long)left*left==num)return true;
        else return false;
    }
};c

移除元素

27. 移除元素 - 力扣（LeetCode）

此题是双指针的典型例题，当然用暴力遍历也可。此题快指针的作用是寻找新数组的元素，新数组就是不含有目标元素的数组，慢指针的作用是指向更新新数组下标的位置。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int left = 0;
        for(int i=0;i<nums.size();i++){
            if(nums[i]!=val){
                nums[left]=nums[i];
                left++;
            }
            else continue;
        }
        return left;
    }
};

26. 删除有序数组中的重复项 - 力扣（LeetCode）

此题和上一题很像，也是双指针思路，唯一的不同在于判断条件不同，并且还是比较难理解的。此题慢指针left维护的是前left个元素是不同的元素。

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int left = 1;
        int n = nums.size();
        for(int i=1;i<nums.size();i++){
            if(nums[i]==nums[i-1])n--;
            else{
                nums[left]=nums[i];
                left++;
            }
        }
        return n;
    }
};

283. 移动零 - 力扣（LeetCode）

此题和27. 移除元素 - 力扣（LeetCode）很像，相当于我们寻找的目标元素是0，但要求不是把0删除，而是放到数组后面，因此此题不会使用覆盖操作，而是使用交换操作。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int left = 0;
        for(int i=0;i<nums.size();i++){
            if(nums[i]==0)continue;
            else{
                swap(nums[left],nums[i]);
                left++;
            }
        }
    }
};

844. 比较含退格的字符串 - 力扣（LeetCode）

此题也可以使用双指针来做，其实与27. 移除元素 - 力扣（LeetCode）还是很像，相当于我们寻找的目标元素是“#”，当我们找到目标元素“#”时，我们不仅要把它删除，还要把它前一个元素也要删除。这种操作体现在代码中就是把左指针往前移动。

class Solution {
public:
    string backspacestring(string ss){
        int left = 0;
        for(int i=0;i<ss.size();i++){
            if(ss[i]!='#'){
                ss[left]=ss[i];
                left++;
            }
            else if(left>0)left--;//把前面一个元素删除，删除之前要判断前面是否还有元素
        }
        ss.resize(left);//将后面不要的元素删除
        return ss;
    }
    bool backspaceCompare(string s, string t) {
        return backspacestring(s)==backspacestring(t);
    }
};

此题还可以借助栈来重构字符串解决问题，具体而言，就是遍历字符串，如果当前字符不是“#”，就直接压入栈中，如果是“#”，就将栈顶元素弹出。值得一提的是，我们不需要真的使用栈，用字符串来模拟即可。由于使用了新的空间，故空间复杂度就不是 $O(1)$ 了。

class Solution {
public:
    string backspacestring(string ss){
        string ans="";
        for(int i=0;i<ss.size();i++){
            if(ss[i]!='#')ans.push_back(ss[i]);
            else if(ans.size()!=0){
                ans.pop_back();
            }
        }
        return ans;
    }
    bool backspaceCompare(string s, string t) {
        return backspacestring(s)==backspacestring(t);
    }
};

977. 有序数组的平方 - 力扣（LeetCode）

此题暴力的方法就是直接使用sort进行排序，时间复杂度为 $O(nlogn)$ 。时间复杂度要为 $O(n)$ ,肯定得使用双指针。双指针有两种思路，第一种是找到数组的正负分界点，从分界点开始，进行左右比较，将平方后较小的元素放入答案数组中。此外，这种方法要进行边界处理，当左右两边有一边没有元素时，就不用比较了，直接把剩下一边的元素的平方加入数组。第二种就是直接比较数组的两头，将较大的元素加入答案数组中。这种方法较第一种方法比较简单，因为不需要边界处理了。

//比较两头的双指针
class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int>ans;
        int left = 0;
        int right = nums.size()-1;
        while(left<=right){
            if(nums[left]*nums[left]<=nums[right]*nums[right]){
                ans.push_back(nums[right]*nums[right]);
                right--;
            }
            else{
                ans.push_back(nums[left]*nums[left]);
                left++;
            }
        }
        reverse(ans.begin(),ans.end());
        return ans;
    }
};

长度最小的子数组

209. 长度最小的子数组 - 力扣（LeetCode）

此题是滑动窗口的典型例题。在想到滑动窗口前，我们首先一定会想到使用暴力算法，即用两层循环，枚举每一个子集合，判断是否满足条件并记录下最短的子集合，这种方法的时间复杂度肯定是为 $O(n^2)$ 。从时间复杂度出发，我们如何缩短时间复杂度？其实从暴力算法来看，暴力算法枚举了一些肯定不是最终答案的子集合。例如在下图中，假设target=10 ，此时start到end正好是一个满足条件的子集合。按照暴力算法的思路，下一个枚举的集合就是从start到end+1。然而，仔细思考，其实我们没有必要在枚举这个集合了，因为这个集合的长度肯定比上一个集合长，所以肯定不会是最终的答案，所以说枚举这个集合是没有必要的。暴力算法就是枚举了很多这种没有必要枚举的集合才使得时间复杂度为 $O(n^2)$ 。

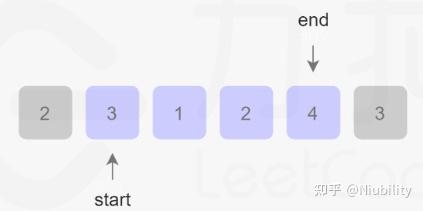
此题最好的解题方法便是滑动窗口了，其时间复杂度为 $O(n)$ ，因为相较于暴力算法，其很大程度上减少了无效枚举。举一个例子说明，还是以上图为例，此时的集合是3 1 2 4，滑动串口下一阶段枚举的是1 2 4 而不是3 1 2 4 3(暴力算法下一阶段)。其实滑动窗口本质上还是一种双指针，快指针代表枚举的子集合的右端点，而慢指针代表左端点。当子集合满足条件时，就移动左端点，反之移动右端点。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int left = 0;
        int ans = 1e9;
        int sum = 0;
        for(int i=0;i<nums.size();i++){
            sum+=nums[i];
            while(sum>=target){
                int sublen = i-left+1;
                ans = min(ans,sublen);
                sum-=nums[left];
                left++;
            }
        }
        if(ans!=1e9)return ans;
        else return 0;
    }
};

904. 水果成篮 - 力扣（LeetCode）

此题和209. 长度最小的子数组 - 力扣（LeetCode）很像，判断条件由子集合总和变成了子集合中有多少类。此题仍然可采用滑动窗口，当集合中的种类数小于等于2时，继续移动快指针，反之移动慢指针。此题可通过维护一个vector来判断集合中有多少类。

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        vector<int>map(fruits.size());//记录每种水果有多少个
        int left = 0;
        int ans = -1;
        int kind = 0;//集合中种类
        for(int i=0;i<fruits.size();i++){
            map[fruits[i]]++;
            if(map[fruits[i]]==1)kind++;
            while(kind>2){
                map[fruits[left]]--;
                if(map[fruits[left]]==0)kind--;
                left++;
            }
            ans = max(ans,i-left+1);
        }
        return ans;
    }
};

76. 最小覆盖子串 - 力扣（LeetCode）

此题和904. 水果成篮 - 力扣（LeetCode）还是比较像的，此题的字符种类就好比是水果的种类，但此题还有数量要求。整体的思路和上一题没什么区别，此题使用了两个哈希表分别表示枚举的集合和目标集合，在判断枚举集合是否满足目标集合时，可以通过一个函数完成。

注：如果我将t_map和s_map设置为局部变量，再实现函数isWindow()貌似会超时，不知道什么原因。

class Solution {
public:
    unordered_map<char,int>t_map;
    unordered_map<char,int>s_map;
    bool isWindow(){
        for(auto it:t_map){
            if(s_map[it.first]<it.second)return false;
        }
        return true;
    }
    string minWindow(string s, string t) {
        int index1=-1;
        int ans = 1e9;
        int left=0;
        for(int i=0;i<t.size();i++)t_map[t[i]]++;
        for(int i=0;i<s.size();i++){
            s_map[s[i]]++;
            while(isWindow()){
                int len = i-left+1;
                if(len<ans){
                    ans = len;
                    index1=left;
                }
                s_map[s[left]]--;
                left++;
            }
        }
        if(ans!=1e9)return s.substr(index1,ans);
        else return "";
    }

螺旋矩阵II

59. 螺旋矩阵 II - 力扣（LeetCode）

此题是一个模拟题，没写过的还真有点难度，很容易写混乱，模拟过程就是一圈一圈的填充数字，每一圈都拆分为对四条边分别进行填充数字，并且填充四条边时都遵循左闭右开原则。此外，无论n是奇数还是偶数，填充的圈数都是n/2，唯一不同的是，奇数较偶数需要最后处理中间的一个点，（可以证明的，当然也可以画几个矩阵试一下）。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>>ans(n,vector<int>(n));
        int sum = n/2;
        int start_x=0;//起始位置x下标
        int start_y=0;//起始位置y下标
        int i=0;
        int j=0;
        int offset = 1;//循环次数
        int count = 1;//计数
        while(sum--){
            for(j=start_y;j<n-offset;j++){
                ans[start_x][j]=count;
                count++;
            }
            for(i=start_x;i<n-offset;i++){
                ans[i][j]=count;
                count++;
            }
            for(;j>start_y;j--){
                ans[i][j]=count;
                count++;
            }
            for(;i>start_x;i--){
                ans[i][j]=count;
                count++;
            }
            start_x++;
            start_y++;
            offset++;
        }
        if(n%2==0)return ans;
        else{
            ans[start_x][start_y]=count;
            return ans;
        }
    }
};

54. 螺旋矩阵 - 力扣（LeetCode）

此题是59. 螺旋矩阵 II - 力扣（LeetCode）的变式题，唯一不同的是矩阵不再是方阵，而是一个普通的矩阵。因此要分情况对矩阵的行数和列数进行讨论。此题有几个小结论：1.循环填充的次数等于min(m,n)；2.矩阵的行数m更小且为奇数时，最后会剩下一行；3.矩阵的列数n更小且为奇数时，最后会剩下一列。此外，在最后的处理阶段，我们的区间遍历要从左闭右开变为左闭右闭。

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int>ans;
        int i=0;
        int j=0;
        int start_x=0;
        int start_y=0;
        int offet=1;
        int m = matrix.size();
        int n = matrix[0].size();
        int sum=min(m,n)/2;
        while(sum--){
            for(j=start_y;j<n-offet;j++)ans.push_back(matrix[start_x][j]);
            for(i=start_x;i<m-offet;i++)ans.push_back(matrix[i][j]);
            for(;j>start_y;j--)ans.push_back(matrix[i][j]);
            for(;i>start_x;i--)ans.push_back(matrix[i][j]);
            start_x++;
            start_y++;
            offet++;
        }
        //行数更少且为奇数，最后会剩下一行，由于只遍历一次，则区间是左闭右闭，与上面的循环块不同
        if(m==min(m,n)&&m%2!=0){
            for(j=start_y;j<n-offet+1;j++)ans.push_back(matrix[start_x][j]);
        }
        //列数更少且为奇数，最后会剩下一列，由于只遍历一次，则区间是左闭右闭，与上面的循环块不同
        else if(n==min(m,n)&&n%2!=0){
            for(i=start_x;i<m-offet+1;i++)ans.push_back(matrix[i][start_y]);
        }
        return ans;
    }
};

LCR 146. 螺旋遍历二维数组 - 力扣（LeetCode）

此题和54. 螺旋矩阵 - 力扣（LeetCode）几乎完全相同，唯一需要注意的是此题需要进行特判，因为此题的矩阵可能是空的，如果我们对空矩阵求列数，就会报错。

class Solution {
public:
    vector<int> spiralArray(vector<vector<int>>& array) {
        vector<int>ans;
        if(array.size()==0||array[0].size()==0)return ans;
        int startx = 0;
        int starty = 0;
        int i,j=0;
        int m = array.size();
        int n = array[0].size();
        int minn = min(m,n);
        int sum = minn/2;
        int offset = 1;
        while(sum--){
            for(j=starty;j<n-offset;j++)ans.push_back(array[startx][j]);
            for(i=startx;i<m-offset;i++)ans.push_back(array[i][j]);
            for(;j>starty;j--)ans.push_back(array[i][j]);
            for(;i>startx;i--)ans.push_back(array[i][j]);
            startx++;
            starty++;
            offset++;
        }
        if(minn==m&&m%2!=0){
            for(int k=starty;k<n-offset+1;k++)ans.push_back(array[startx][k]);
        }
        else if(minn==n&&n%2!=0){
            for(int k=startx;k<m-offset+1;k++)ans.push_back(array[k][starty]);
        }
        return ans;    
    }
};

Share on

Twitter Facebook LinkedIn

LiFei